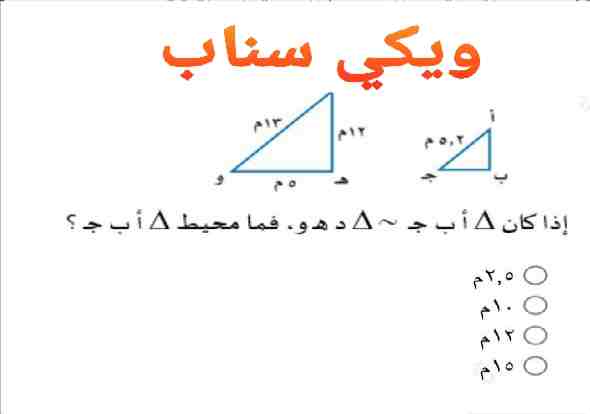
إذا كان △ أ ب جـ ~ △ د هـ و ، فما محيط △ أ ب جـ ؟
في البداية، لكي نحسب محيط المثلث أ ب جـ ، يجب علينا أولاً التأكد من أنه يشترك بنفس النسبة مع المثلث د هـ و.
بعد ذلك إذا كانت النسبة بين الأضلاع في المثلثين متساوية، فإنهما متشابهان ولهما نفس الأشكال الداخلية.
ثم سنكتب النسبة بالشكل التالي:
△ أ ب جـ ~ △ د هـ
كذلك، وبالاستناد إلى وجود هذه النسبة المتساوية، يمكننا القول أن النسبة بين أضلاع المثلثين متساوية هي: أ ب / د هـ = ب جـ / هـ
في الختام، لإيجاد محيط المثلث أ ب جـ ، يمكننا استخدام النسبة لتحويل أي ضلع من المثلث د هـ إلى أ و شجرة، ثم جمع الأضلاع الثلاثة.
أو بـ ج = (أ ب / د هـ) × هـ
إجابة السؤال: إذا كان △ أ ب جـ ~ △ د هـ و ، فما محيط △ أ ب جـ ؟
٢،٥ م
١٠ م
١٢ م
١٥ م
الجواب الصحيح هو : ١٢ م.